Algoritm (romana)

                  BUTOIUL BULGAR

     Jocul este conceput pentru a contribui la dezvoltarea logicii, memoriei şi imaginaţie spaţiale a copiilor, oferind o oportunitate plăcută de distracţie pentru adulţi.
Materialele din care este produsă jucăria sunt permise pentru contact cu copii.

Suprafeţele pot fi curăţate cu o cârpă umedă şi preparatele care conţin alcool, dar în nici un caz, acetonă, corselină şi dizolvant pentru lacul de unghii.
Dacă nu se foloseşte o perioada mai lungă de timp, sectoarele trebuie să fie aparte de suprafaţa de separare pentru fixatorii interiori.

               Algoritm de aranjare

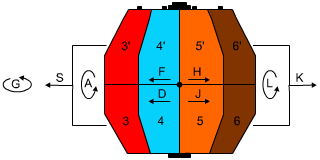
     Pentru simplificare introducem următoarele indicaţii a mişcărilor posibile
F - mişcarea sectoarelor în jumătatea de sus în stângă
H - mişcarea sectoarelor în jumătatea de sus în dreaptă
D - mişcarea sectoarelor în jumătatea de jos în stângă
J - mişcarea sectoarelor în jumătatea de sus în dreaptă
A – rotirea jumătăţii din stângă la 180°
L - rotirea jumătăţii din stângă la 180°
S – rotirea simultană a sectoarelor în jumătatea de jos şi sus în stângă
K - rotirea simultană a sectoarelor în jumătatea de jos şi sus în dreaptă
G – rotirea sectorului de ecuator la 180°
După F, H, D şi J apare o cifră, care înseamnă numărul paşilor.

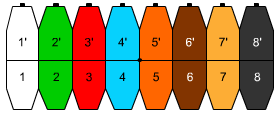
       Extinderea sectoarelor

1. Schimbarea locurilor culorilor a două culori învecinate, fără a schimba locul altor culori.

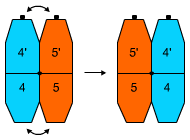
                 Formula 1
       А, F1, A, H1, D1, A, J1, A

2. Schimbarea locurilor a doar două sectoare adiacente.

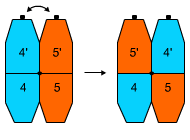
                 Formula 2
               A , F1, A, H1, A

     Înainte de ultima mişcare А, cuplul din stângă 5'/4 este aranjat, dar cu coroană în jos şi numărul coroanelor din fiecare parte este impar.
Această schimbare şi această condiţie stau la baza algoritmului. Cu ea se pot schimba atât unu cât şi două culori simultan, dar la fiecare schimbare întotdeauna se schimbă paritatea coroanelor de la o parte şi de la altă.
Un exerciţiu de aranjare de exemplu arată aşa:
1. Sectoarele cu  coroana sunt în partea superioară.
2. Culoarele să fie în ordinea selectată de Dvs.
3. Coroana corpului să fie întreagă şi în partea superioară.

     Aranjarea se face în trei etape:
1.Adunarea sectoarelor cu coroanele sus.
Sectoarele se pun cu coroană în poziţie 1' şi poziţie 5, se efectuează  L; H1 şi ambele sectoare cu coroană se aranjează unul lângă altul. Aceasta se face şi cu restul, dar când sus rămâne numai un sector fără coroana, acesta se pune în poziţie 4'. Ultimul sector cu coroană, care se află jos se pune în poziţie 5, se efectuează L; H1; L şi toate sectoarele cu coroană se adună sus.
2. Aranjarea sectoarelor cu aceiași culoare unu peste altul, iar ordinea culorilor este aleatoare.

Pentru acest scop se folosesc ambele formule, dar succesul fina depinde de următoarea condiţie importantă:
Suma numărului de sectoare cu coroană dintr-o parte şi numărul schimbărilor rămase după formula 2. să fie un număr PAR .
Dacă suma este un număr nepar şi se continuă cu schimbări după formula 2, culorile se vor aranja, dat o culoare va rămâne cu coroană inversă. Pentru a evita aceasta este necesar un oas suplimentar, iar calcularea se face după aranjarea a 3 sau 4 culori. .
Vom analiza şi un exemplu, când suma este un număr nepar.

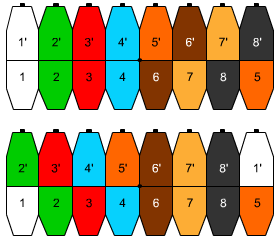
      Coroanele în partea de sus sunt 8, aranjate în patru culori (1,2,3,4) şi rămân câte 3 schimbări după formula 2., pentru ca la următoarea se vor aranja două culori simultan. Culorile se vor aranja, dar o culoare va rămâne cu coroana inversă, pentru că suma este 8+3=11.


      Pentru a evita acest lucru se efectuează F1 şi se aranjează 3 culori (6,7,8), iar următoarele 5 culoare (1,2,3,4,5) se amestecă sincron şi numai la pasul 1.
Coroanele rămân 8, dar pentru cele cinci culori nu sunt necesare 4 mutări cu formulă 2 Suma este 8+4=12 şi etapa poate fi finalizata.
Opțiunile pentru utilizarea acestei tehnici sunt multe, dar scopul este întotdeauna unul - realizarea parității sumei.
Dacă omiteţi momentul potrivit şi suma rămâne nepară, se aranjează toate culorile indiferent, că o culoare va fi cu coroana întoarsă. Se efectuează odată formula 2 şi după aceasta F1. O culoare se aranjează în poziţie 4, iar cele 7 culori se amestecă, dar sincron la un pas. Coroanele întoarse devin un număr par, iar schimbările necesare cu formula 2 sunt 6.

    Numărul total este un număr par şi aranjarea se finalizează.

3. Aranjarea rândului de culori, ales de dvs.
Aceasta etapă se efectuează cu schimbări după formula 1, iar Numărul lor depinde numai de inteligența Dumneavoastră.
4. Aranjarea coroanei corpului.
Dacă toate culoarele sunt aranjate, dar jumătatea coronei corpului este întoarsă se urmăresc paşii A, F4, A, F4, A.
Cu aceasta exerciţiul este îndeplinit şi noi Vă felicită cu acest succes!
 

    Calcularea numărul total de variante între elementele jocului::
Sectoarele sunt 16, iar denumirea exactă a acestor combinaţii în matematică este permutaţie, iar numărul lor total este: P₁₆=16!=1x2x3...15x16=20,9x10¹²
Variantele de aranjamentul final a celor opt culori este, de asemenea, o permutare, iar numărul lor este: P₈=8!=1x2x3x4x5x6x7x8=40320
Această diversitate exclude folosirea algoritmului mecanic și necesită o abordare creativa pentru fiecare mişcare, iar contribuţia principală pentru timpul minim obţinut are nu dexteritatea, ci înainte de toate inteligența dumneavoastră.

Campionii joacă, dar, au nevoie şi de un public! Alegerea este a Dvs.!

        VĂ DORIM SUCCES !