Bulgarian burentse
The game is designed to help develop logic, memory and spatial imagination of children by providing a pleasant opportunity for entertainment of adults also.
The materials used to producethe toysare allowedforcontact with children.
Surfaces can be cleaned with a damp cloth and preparations containing alcohol, but never useacetone,nail polish remover and koreselin.
For longer stays, the sectors must be off the pitch surface, so as not to burden the internal latch.
Algorithm for arrangement
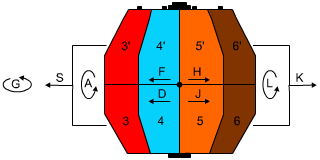
For convenienceweintroduce the following indications of possible movements
F - movement of the sectors in the upper half to the left
H - movement of the sectors in the upper half to the right
D - movement of the sectors in the lower half to the left
J - movement of the sectors in the bottom half to the right
A - left side rotationat180 °
L - rotation of the right half at180 °
S - movement of both sectors in the upper and lower half to the left
K - movement of both sectors in the upper and lower half to the right
G - equator separator rotation at 180 °
After F, H, D and J put a figure denoting the number of steps.
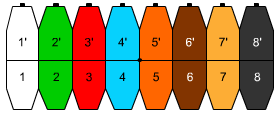
Unfoldi ng of the sectors
1. Changing the locations of two adjacent colors without changing the locations oftheother colors.
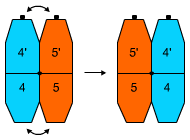
Formula 1
A, F1, A, H1, D1, A, J1, A
2. Changing the locations ofonly two adjacent sectors.
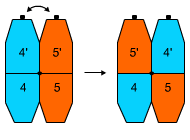
Formula 2
A, F1, A, H1, A
Before the lastmoveA,the left couple 5 '/ 4 is arranged, but the crown down and the number of crowns on each side is odd.
This shift and thisconditionarethat underlie the algorithm. Using that algorithm the kegcan be arranged as one and two colors simultaneously, but each arrangement is always changing parity of the crowns andon one or theotherside.
One example task arrangement is as follows:
1. Sectors withthe crownareat the top.
2. The colors are in orderof your choice.
3. Crown of the hull is intact and at the top.
The arrangement is in 3 phases:
1. Collection of sectors with the crownsabove.
Install the sector with a crown of pos.1 'and pos.5, executed, L; H1 and the two sectors with a crown are placed side by side. This is done with othersalso, but at the top remainsonly one sector without the crown, it shall be placedon Pos. 4 '. The last sector with a crown, which is located below, is placed in pos.5. Run L; H1; L and all sectors with a crown are collected at the top.
2. Arrangementof sectors with the same color above each other, the order of colors is arbitrary.
For this purpose, using both formulas, but ultimate success depends on the following important condition:
Sum of the number of sectors with a crown on one side and the number of remaining shifts in formula 2.be even.
If the sum is odd and continue with the change in formula 2., the colors will be arranged, but one will remain with the crown back. To avoid this, an additional moveis needed, but the calculation is made after the arrangement of 3 or 4 colors.
We'll look at an example where the sum is odd.
The crowns the topare8,four colorsare arranged(1,2,3,4) and only3 shiftsremainin formula 2.,cecause at the last arrangementwill be 2 colors simultaneously. The colors will be arranged, but one will remain inverted crown because the sum is 8 +3 = 11.
To avoid this run F1 and stacked 3 colors(6,7,8), az the remaining5 colors (1,2,3,4,5) shallbe moved synchronously and onlyinone step.
The crownsremains 8, but for the five colors are now needed four shifts in formula 2. The sum is 8 +4 = 12 and phase can be completed.
The options for using this technique are many, but the goal always is one - achieving parity of the sum.
If you miss the right moment and the sum remains odd, all colors will bearranged, although one will remain with the inverted crown. Run formula 2onesand then F1. One color is arranged in position 4, while the other 7 colors mix, butinone synchronous step. Inverted crowns are an even number, and the necessary change in formula 2 are 6. The total number is even number and arrangement can be completed.
3. Arrange your chosen line of colors.
This stage takes place onlywithchangesin Formula 1. And their number depends only on your wits.
4. Arrangementof the Crown case.
If all colors are arranged, but half of thecrownson the body areturneddown, run A, F4, A, F4, A.
This ishowthe task is completeand we congratulateyou withthe success!
Count the total number of variations between elements of the game:
Sectors are 16 pieces, the exact name in the mathematics of such compound is permutation, but their total number is: P 16 = 16! = 1x2x3 ... 15x16 = 20,9 x10 12
Variations of final arrangement of eight colors is also permutation, and the number is: P = 8 8! = 1x2x3x4x5x6x7x8 = 40320
This diversity precludes the use of mechanical algorithm and requires a creative approach to every move by a major contribution to those achieved minimum time has no skill, but above all your intelligence.



